Working with the public 10-year IceCube point-source data
This tutorial shows how to use the IceCube public 10-year point-source data with SkyLLH.
Disclaimer
The released 10-year IceCube point-source data can reproduce the published results only within a certain
amount of uncertainty due to the limited instrument response function binning provided in the data release.
The IceCube collaboration is able to reproduce the published results using detailed direct simulation
data, as done for the publication.
[1]:
%load_ext autoreload
%autoreload 2
[2]:
import numpy as np
from matplotlib import pyplot as plt
Getting the datasets
First we import the dataset definition of the public 10-year point-source data set:
[3]:
from skyllh.datasets.i3.PublicData_10y_ps import create_dataset_collection
The collection of datasets can be created using the create_dataset_collection function. This function requires the base path to the data repository. It’s the path where the public point-source data is stored. The public point-source data can be downloaded from the IceCube website.
[4]:
dsc = create_dataset_collection(base_path='/home/mwolf/projects/publicdata_ps/')
The dataset_names property provides a list of all the data sets defined in the data set collection of the public point-source data.
[5]:
dsc.dataset_names
[5]:
['IC40',
'IC59',
'IC79',
'IC86_I',
'IC86_II',
'IC86_II-VII',
'IC86_III',
'IC86_IV',
'IC86_V',
'IC86_VI',
'IC86_VII']
The individual data sets IC86_II, IC86_III, IC86_IV, IC86_V, IC86_VI, and IC86_VII are also available as a single combined data set IC86_II-VII, because these data sets share the same detector simulation and event selection. Hence, we can get a list of data sets via the get_datasets method of the dsc instance:
[6]:
datasets = dsc.get_datasets(['IC40', 'IC59', 'IC79', 'IC86_I', 'IC86_II-VII'])
Getting the analysis
The analysis used for the published PRL results is referred in SkyLLH as “traditional point-source analysis” and is pre-defined:
[7]:
from skyllh.analyses.i3.publicdata_ps.time_integrated_ps import create_analysis
[8]:
help(create_analysis)
Help on function create_analysis in module skyllh.analyses.i3.publicdata_ps.time_integrated_ps:
create_analysis(datasets, source, refplflux_Phi0=1, refplflux_E0=1000.0, refplflux_gamma=2, ns_seed=10.0, gamma_seed=3, kde_smoothing=False, minimizer_impl='LBFGS', cap_ratio=False, compress_data=False, keep_data_fields=None, optimize_delta_angle=10, tl=None, ppbar=None)
Creates the Analysis instance for this particular analysis.
Parameters:
-----------
datasets : list of Dataset instances
The list of Dataset instances, which should be used in the
analysis.
source : PointLikeSource instance
The PointLikeSource instance defining the point source position.
refplflux_Phi0 : float
The flux normalization to use for the reference power law flux model.
refplflux_E0 : float
The reference energy to use for the reference power law flux model.
refplflux_gamma : float
The spectral index to use for the reference power law flux model.
ns_seed : float
Value to seed the minimizer with for the ns fit.
gamma_seed : float | None
Value to seed the minimizer with for the gamma fit. If set to None,
the refplflux_gamma value will be set as gamma_seed.
kde_smoothing : bool
Apply a KDE-based smoothing to the data-driven background pdf.
Default: False.
minimizer_impl : str | "LBFGS"
Minimizer implementation to be used. Supported options are "LBFGS"
(L-BFG-S minimizer used from the :mod:`scipy.optimize` module), or
"minuit" (Minuit minimizer used by the :mod:`iminuit` module).
Default: "LBFGS".
cap_ratio : bool
If set to True, the energy PDF ratio will be capped to a finite value
where no background energy PDF information is available. This will
ensure that an energy PDF ratio is available for high energies where
no background is available from the experimental data.
If kde_smoothing is set to True, cap_ratio should be set to False!
Default is False.
compress_data : bool
Flag if the data should get converted from float64 into float32.
keep_data_fields : list of str | None
List of additional data field names that should get kept when loading
the data.
optimize_delta_angle : float
The delta angle in degrees for the event selection optimization methods.
tl : TimeLord instance | None
The TimeLord instance to use to time the creation of the analysis.
ppbar : ProgressBar instance | None
The instance of ProgressBar for the optional parent progress bar.
Returns
-------
analysis : TimeIntegratedMultiDatasetSingleSourceAnalysis
The Analysis instance for this analysis.
As source we use TXS 0506+056.
[9]:
from skyllh.physics.source import PointLikeSource
[10]:
source = PointLikeSource(ra=np.deg2rad(77.35), dec=np.deg2rad(5.7))
[11]:
ana = create_analysis(datasets=datasets, source=source)
[==========================================================] 100% ELT 0h:00m:14s[ ] 0% ELT 0h:00m:00s
[==========================================================] 100% ELT 0h:00m:13s[ ] 0% ELT 0h:00m:00s
[==========================================================] 100% ELT 0h:00m:13s[ ] 0% ELT 0h:00m:00s
[==========================================================] 100% ELT 0h:00m:13s[ ] 0% ELT 0h:00m:00s
[==========================================================] 100% ELT 0h:00m:12s[ ] 0% ELT 0h:00m:00s
[==========================================================] 100% ELT 0h:01m:36s
[==========================================================] 100% ELT 0h:00m:00s
Initializing a trial
After the Analysis instance was created trials can be run. To do so the analysis needs to be initialized with some trial data. For instance we could initialize the analysis with the experimental data to “unblind” the analysis afterwards. Technically the TrialDataManager of each log-likelihood ratio function, i.e. dataset, is initialized with data.
The Analysis class provides the method initialize_trial to initialize a trial with data. It takes a list of DataFieldRecordArray instances holding the events. If we want to initialize a trial with the experimental data, we can get that list from the Analysis instance itself:
[32]:
events_list = [ data.exp for data in ana.data_list ]
ana.initialize_trial(events_list)
Maximizing the log-likelihood ratio function
After initializing a trial, we can maximize the LLH ratio function using the maximize_llhratio method of the Analysis class. This method requires a RandomStateService instance in case the minimizer does not succeed and a new set of initial values for the fit parameters need to get generated. The method returns a 4-element tuple. The first element is the set of fit parameters used in the maximization. The second element is the value of the LLH ration function at its maximum. The third
element is the array of the fit parameter values at the maximum, and the forth element is the status dictionary of the minimizer.
[39]:
from skyllh.core.random import RandomStateService
rss = RandomStateService(seed=1)
[40]:
(fitparamset, log_lambda_max, fitparam_values, status) = ana.maximize_llhratio(rss)
[44]:
print(f'log_lambda_max = {log_lambda_max}')
print(f'fitparam_values = {fitparam_values}')
print(f'status = {status}')
log_lambda_max = 6.572529558548655
fitparam_values = [14.58039149 2.1685849 ]
status = {'grad': array([-2.09454353e-06, 2.13693588e-04]), 'task': b'CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH', 'funcalls': 15, 'nit': 9, 'warnflag': 0, 'skyllh_minimizer_n_reps': 0, 'n_llhratio_func_calls': 15}
Calculating the test-statistic
Using the maximum of the LLH ratio function and the fit parameter values at the maximum we can calculate the test-statistic using the calculate_test_statistic method of the Analysis class:
[48]:
TS = ana.calculate_test_statistic(log_lambda_max, fitparam_values)
print(f'TS = {TS:.3f}')
TS = 13.145
Unblinding the data
After creating the analysis instance we can unblind the data for the choosen source. Hence, we initialize the analysis with a trial of the experimental data, maximize the log-likelihood ratio function for all given experimental data events, and calculate the test-statistic value. The analysis instance has the method unblind that can be used for that. This method requires a RandomStateService instance in case the minimizer does not succeed and a new set of initial values for the fit
parameters need to get generated.
[35]:
from skyllh.core.random import RandomStateService
rss = RandomStateService(seed=1)
[13]:
help(ana.unblind)
Help on method unblind in module skyllh.core.analysis:
unblind(rss) method of skyllh.core.analysis.TimeIntegratedMultiDatasetSingleSourceAnalysis instance
Evaluates the unscrambled data, i.e. unblinds the data.
Parameters
----------
rss : RandomStateService instance
The RandomStateService instance that should be used draw random
numbers from.
Returns
-------
TS : float
The test-statistic value.
fitparam_dict : dict
The dictionary holding the global fit parameter names and their best
fit values.
status : dict
The status dictionary with information about the performed
minimization process of the negative of the log-likelihood ratio
function.
The unblind method returns the test-statistic value, the best-fit fit parameter values, and a status dictionary of the minimizer.
[14]:
(ts, x, status) = ana.unblind(rss=rss)
[15]:
print(f'TS = {ts:.3f}')
print(f'ns = {x["ns"]:.2f}')
print(f'gamma = {x["gamma"]:.2f}')
TS = 13.145
ns = 14.58
gamma = 2.17
Calculating the corresponding flux normalization
By default the analysis is created with a flux normalization of 1 GeV\(^{-1}\)s\(^{-1}\)cm\(^{-2}\)sr\(^{-1}\) (see refplflux_Phi0 argument of the create_analysis method). The analysis instance has the method calculate_fluxmodel_scaling_factor that calculates the scaling factor the reference flux normalization has to be multiplied with to represent a given analysis result, i.e. \(n_{\text{s}}\) and \(\gamma\) value. This function takes the
detected mean \(n_{\text{s}}\) value as first argument and the list of source parameter values as second argument:
[16]:
scaling_factor = ana.calculate_fluxmodel_scaling_factor(x['ns'], [x['gamma']])
print(f'Flux scaling factor = {scaling_factor:.3e}')
Flux scaling factor = 1.423e-15
Hence, our result corresponds to a power-law flux of:
[17]:
print(f'{scaling_factor:.3e}'' (E/1000 GeV)^{-'f'{x["gamma"]:.2f}'+'} 1/(GeV s cm^2 sr)')
1.423e-15 (E/1000 GeV)^{-2.17} 1/(GeV s cm^2 sr)
Evaluating the log-likelihood ratio function
Sometimes it is useful to be able to evaluate the log-likelihood ratio function, e.g. for creating a likelihood contour plot. Because SkyLLH’s structure is based on the mathematical structure of the likelihood function, the Analysis instance has the property llhratio which is the class instance of the used log-likelihood ratio function. This instance has the method evaluate. The method takes an array of the fit parameter values as argument at which the LLH ratio function will be
evaluated. It returns the value of the LLH ratio function at the given point and its gradients w.r.t. the fit parameters.
In our case this is the number of signal events, \(n_{\mathrm{s}}\) and the spectral index \(\gamma\). If we evaluate the LLH ratio function at the maximum, the gradients should be close to zero.
[31]:
help(ana.llhratio.evaluate)
Help on method evaluate in module skyllh.core.llhratio:
evaluate(fitparam_values, tl=None) method of skyllh.core.llhratio.MultiDatasetTCLLHRatio instance
Evaluates the composite log-likelihood-ratio function and returns its
value and global fit parameter gradients.
Parameters
----------
fitparam_values : (N_fitparams)-shaped numpy 1D ndarray
The ndarray holding the current values of the global fit parameters.
The first element of that array is, by definition, the number of
signal events, ns.
Returns
-------
log_lambda : float
The calculated log-lambda value of the composite
log-likelihood-ratio function.
grads : (N_fitparams,)-shaped 1D ndarray
The ndarray holding the gradient value of the composite
log-likelihood-ratio function for ns and each global fit parameter.
By definition the first element is the gradient for ns.
[29]:
(llhratio_value, (grad_ns, grad_gamma)) = ana.llhratio.evaluate([14.58, 2.17])
print(f'llhratio_value = {llhratio_value:.3f}')
print(f'grad_ns = {grad_ns:.3f}')
print(f'grad_gamma = {grad_gamma:.3f}')
llhratio_value = 6.573
grad_ns = 0.001
grad_gamma = -0.027
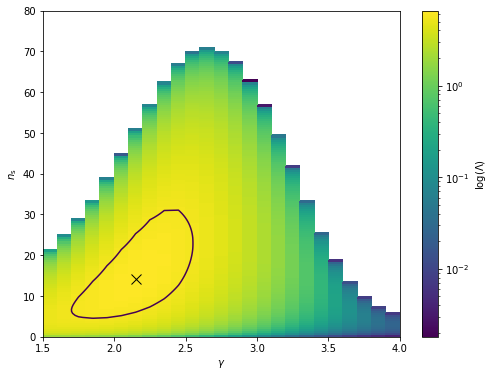
Using the evaluate method of the LLHRatio class we can scan the log-likelihood ratio space and create a contour plot showing the best fit and the 95% quantile.
[136]:
(ns_min, ns_max, ns_step) = (0, 80, 0.5)
(gamma_min, gamma_max, gamma_step) = (1.5, 4.0, 0.1)
ns_edges = np.linspace(ns_min, ns_max, int((ns_max-ns_min)/ns_step)+1)
ns_vals = 0.5*(ns_edges[1:] + ns_edges[:-1])
gamma_edges = np.linspace(gamma_min, gamma_max, int((gamma_max-gamma_min)/gamma_step+1))
gamma_vals = 0.5*(gamma_edges[1:] + gamma_edges[:-1])
log_lambda = np.empty((len(ns_vals), len(gamma_vals)), dtype=np.double)
for (ns_i, ns) in enumerate(ns_vals):
for (gamma_i, gamma) in enumerate(gamma_vals):
log_lambda[ns_i,gamma_i] = ana.llhratio.evaluate([ns, gamma])[0]
# Determine the best fit ns and gamma values from the scan.
index_max = np.argmax(log_lambda)
ns_i_max = int(index_max / len(gamma_vals))
gamma_i_max = index_max % len(gamma_vals)
ns_best = ns_vals[ns_i_max]
gamma_best = gamma_vals[gamma_i_max]
[137]:
from matplotlib.colors import LogNorm
plt.figure(figsize=(8,6))
plt.pcolormesh(gamma_edges, ns_edges, log_lambda, norm=LogNorm())
cbar = plt.colorbar()
cbar.set_label(r'$\log(\Lambda)$')
plt.contour(gamma_vals, ns_vals, log_lambda, [np.quantile(log_lambda, 0.95)])
plt.plot(gamma_best, ns_best, marker='x', color='black', ms=10)
plt.xlabel(r'$\gamma$')
plt.ylabel(r'$n_{\mathrm{s}}$')
plt.ylim(ns_min, ns_max)
plt.xlim(gamma_min, gamma_max)
[137]:
(1.5, 4.0)
Calculating the significance (local p-value)
The significance of the source, i.e. the local p-value, can be calculated by generating the test-statistic distribution of background-only data trials, i.e. for zero injected signal events. SkyLLH provides the helper function create_trial_data_file to do that:
[18]:
from skyllh.core.analysis_utils import create_trial_data_file
[19]:
help(create_trial_data_file)
Help on function create_trial_data_file in module skyllh.core.analysis_utils:
create_trial_data_file(ana, rss, n_trials, mean_n_sig=0, mean_n_sig_null=0, mean_n_bkg_list=None, bkg_kwargs=None, sig_kwargs=None, pathfilename=None, ncpu=None, ppbar=None, tl=None)
Creates and fills a trial data file with `n_trials` generated trials for
each mean number of injected signal events from `ns_min` up to `ns_max` for
a given analysis.
Parameters
----------
ana : instance of Analysis
The Analysis instance to use for the trial generation.
rss : RandomStateService
The RandomStateService instance to use for generating random
numbers.
n_trials : int
The number of trials to perform for each hypothesis test.
mean_n_sig : ndarray of float | float | 2- or 3-element sequence of float
The array of mean number of injected signal events (MNOISEs) for which
to generate trials. If this argument is not a ndarray, an array of
MNOISEs is generated based on this argument.
If a single float is given, only this given MNOISEs are injected.
If a 2-element sequence of floats is given, it specifies the range of
MNOISEs with a step size of one.
If a 3-element sequence of floats is given, it specifies the range plus
the step size of the MNOISEs.
mean_n_sig_null : ndarray of float | float | 2- or 3-element sequence of
float
The array of the fixed mean number of signal events (FMNOSEs) for the
null-hypothesis for which to generate trials. If this argument is not a
ndarray, an array of FMNOSEs is generated based on this argument.
If a single float is given, only this given FMNOSEs are used.
If a 2-element sequence of floats is given, it specifies the range of
FMNOSEs with a step size of one.
If a 3-element sequence of floats is given, it specifies the range plus
the step size of the FMNOSEs.
mean_n_bkg_list : list of float | None
The mean number of background events that should be generated for
each dataset. This parameter is passed to the ``do_trials`` method of
the ``Analysis`` class. If set to None (the default), the background
generation method needs to obtain this number itself.
bkg_kwargs : dict | None
Additional keyword arguments for the `generate_events` method of the
background generation method class. An usual keyword argument is
`poisson`.
sig_kwargs : dict | None
Additional keyword arguments for the `generate_signal_events` method
of the `SignalGenerator` class. An usual keyword argument is
`poisson`.
pathfilename : string | None
Trial data file path including the filename.
If set to None generated trials won't be saved.
ncpu : int | None
The number of CPUs to use.
ppbar : instance of ProgressBar | None
The optional instance of the parent progress bar.
tl: instance of TimeLord | None
The instance of TimeLord that should be used to measure individual
tasks.
Returns
-------
seed : int
The seed used to generate the trials.
mean_n_sig : 1d ndarray
The array holding the mean number of signal events used to generate the
trials.
mean_n_sig_null : 1d ndarray
The array holding the fixed mean number of signal events for the
null-hypothesis used to generate the trials.
trial_data : structured numpy ndarray
The generated trial data.
At first we will generate 10k trials and look at the test-statistic distribution. We will time the trial generation using the TimeLord class.
[20]:
from skyllh.core.timing import TimeLord
tl = TimeLord()
[21]:
rss = RandomStateService(seed=1)
(_, _, _, trials) = create_trial_data_file(
ana=ana,
rss=rss,
n_trials=1e4,
mean_n_sig=0,
pathfilename='/home/mwolf/projects/publicdata_ps/txs_bkg_trails.npy',
ncpu=8,
tl=tl)
print(tl)
[==========================================================] 100% ELT 0h:07m:31s
TimeLord: Executed tasks:
[Generating background events for data set 0.] 0.002 sec/iter (10000)
[Generating background events for data set 1.] 0.003 sec/iter (10000)
[Generating background events for data set 2.] 0.003 sec/iter (10000)
[Generating background events for data set 3.] 0.005 sec/iter (10000)
[Generating background events for data set 4.] 0.024 sec/iter (10000)
[Generating pseudo data. ] 0.030 sec/iter (10000)
[Initializing trial. ] 0.030 sec/iter (10000)
[Create fitparams dictionary. ] 1.0e-05 sec/iter (593990)
[Calc fit param dep data fields. ] 2.9e-06 sec/iter (593990)
[Get sig prob. ] 1.8e-04 sec/iter (593990)
[Evaluating bkg log-spline. ] 2.6e-04 sec/iter (593990)
[Get bkg prob. ] 3.2e-04 sec/iter (593990)
[Calc PDF ratios. ] 6.2e-05 sec/iter (593990)
[Calc pdfratio values. ] 8.2e-04 sec/iter (593990)
[Calc pdfratio value product Ri ] 3.5e-05 sec/iter (593990)
[Calc logLamds and grads ] 2.9e-04 sec/iter (593990)
[Evaluate llh-ratio function. ] 0.004 sec/iter (118798)
[Minimize -llhratio function. ] 0.052 sec/iter (10000)
[Maximizing LLH ratio function. ] 0.052 sec/iter (10000)
[Calculating test statistic. ] 3.5e-05 sec/iter (10000)
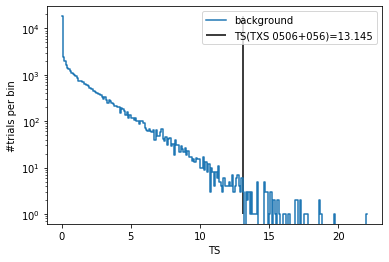
After generating the background trials, we can histogram the test-statistic values and plot the TS distribution.
[22]:
(h, be) = np.histogram(trials['ts'], bins=np.arange(0, np.max(trials['ts'])+0.1, 0.1))
plt.plot(0.5*(be[:-1]+be[1:]), h, drawstyle='steps-mid', label='background')
plt.vlines(ts, 1, np.max(h), label=f'TS(TXS 0506+056)={ts:.3f}')
plt.yscale('log')
plt.xlabel('TS')
plt.ylabel('#trials per bin')
plt.legend()
pass
We can see that the TS value of the unblinded data for TXS is rather large and 10k trials are not enough to calculate a reliable estimate for the p-value. Hence, we will generate a few more trials. SkyLLH provides also a helper function to extend the trial data file we just created. It is called extend_trial_data_file:
[23]:
from skyllh.core.analysis_utils import extend_trial_data_file
[24]:
help(extend_trial_data_file)
Help on function extend_trial_data_file in module skyllh.core.analysis_utils:
extend_trial_data_file(ana, rss, n_trials, trial_data, mean_n_sig=0, mean_n_sig_null=0, mean_n_bkg_list=None, bkg_kwargs=None, sig_kwargs=None, pathfilename=None, **kwargs)
Appends to the trial data file `n_trials` generated trials for each
mean number of injected signal events up to `ns_max` for a given analysis.
Parameters
----------
ana : Analysis
The Analysis instance to use for sensitivity estimation.
rss : RandomStateService
The RandomStateService instance to use for generating random
numbers.
n_trials : int
The number of trials the trial data file needs to be extended by.
trial_data : structured numpy ndarray
The structured numpy ndarray holding the trials.
mean_n_sig : ndarray of float | float | 2- or 3-element sequence of float
The array of mean number of injected signal events (MNOISEs) for which
to generate trials. If this argument is not a ndarray, an array of
MNOISEs is generated based on this argument.
If a single float is given, only this given MNOISEs are injected.
If a 2-element sequence of floats is given, it specifies the range of
MNOISEs with a step size of one.
If a 3-element sequence of floats is given, it specifies the range plus
the step size of the MNOISEs.
mean_n_sig_null : ndarray of float | float | 2- or 3-element sequence of
float
The array of the fixed mean number of signal events (FMNOSEs) for the
null-hypothesis for which to generate trials. If this argument is not a
ndarray, an array of FMNOSEs is generated based on this argument.
If a single float is given, only this given FMNOSEs are used.
If a 2-element sequence of floats is given, it specifies the range of
FMNOSEs with a step size of one.
If a 3-element sequence of floats is given, it specifies the range plus
the step size of the FMNOSEs.
bkg_kwargs : dict | None
Additional keyword arguments for the `generate_events` method of the
background generation method class. An usual keyword argument is
`poisson`.
sig_kwargs : dict | None
Additional keyword arguments for the `generate_signal_events` method
of the `SignalGenerator` class. An usual keyword argument is
`poisson`.
pathfilename : string | None
Trial data file path including the filename.
Additional keyword arguments
----------------------------
Additional keyword arguments are passed-on to the ``create_trial_data_file``
function.
Returns
-------
trial_data :
Trial data file extended by the required number of trials for each
mean number of injected signal events..
[25]:
tl = TimeLord()
rss = RandomStateService(seed=2)
trials = extend_trial_data_file(
ana=ana,
rss=rss,
n_trials=4e4,
trial_data=trials,
pathfilename='/home/mwolf/projects/publicdata_ps/txs_bkg_trails.npy',
ncpu=8,
tl=tl)
[==========================================================] 100% ELT 0h:29m:56s
[26]:
print(tl)
TimeLord: Executed tasks:
[Generating background events for data set 0.] 0.002 sec/iter (40000)
[Generating background events for data set 1.] 0.003 sec/iter (40000)
[Generating background events for data set 2.] 0.003 sec/iter (40000)
[Generating background events for data set 3.] 0.005 sec/iter (40000)
[Generating background events for data set 4.] 0.019 sec/iter (40000)
[Generating pseudo data. ] 0.027 sec/iter (40000)
[Initializing trial. ] 0.032 sec/iter (40000)
[Create fitparams dictionary. ] 1.1e-05 sec/iter (2375320)
[Calc fit param dep data fields. ] 3.3e-06 sec/iter (2375320)
[Get sig prob. ] 2.0e-04 sec/iter (2375320)
[Evaluating bkg log-spline. ] 2.8e-04 sec/iter (2375320)
[Get bkg prob. ] 3.5e-04 sec/iter (2375320)
[Calc PDF ratios. ] 6.8e-05 sec/iter (2375320)
[Calc pdfratio values. ] 8.5e-04 sec/iter (2375320)
[Calc pdfratio value product Ri ] 3.9e-05 sec/iter (2375320)
[Calc logLamds and grads ] 3.1e-04 sec/iter (2375320)
[Evaluate llh-ratio function. ] 0.005 sec/iter (475064)
[Minimize -llhratio function. ] 0.054 sec/iter (40000)
[Maximizing LLH ratio function. ] 0.054 sec/iter (40000)
[Calculating test statistic. ] 3.7e-05 sec/iter (40000)
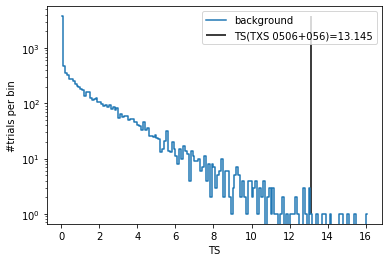
The local p-value is defined as the fraction of background trials with TS value greater than the unblinded TS value of the source.
[27]:
minus_log10_pval = -np.log10(len(trials[trials['ts'] > ts]) / len(trials))
print(f'-log10(p_local) = {minus_log10_pval:.2f}')
-log10(p_local) = 2.93
[28]:
(h, be) = np.histogram(trials['ts'], bins=np.arange(0, np.max(trials['ts'])+0.1, 0.1))
plt.plot(0.5*(be[:-1]+be[1:]), h, drawstyle='steps-mid', label='background')
plt.vlines(ts, 1, np.max(h), label=f'TS(TXS 0506+056)={ts:.3f}')
plt.yscale('log')
plt.xlabel('TS')
plt.ylabel('#trials per bin')
plt.legend()
pass